Mathematics & Statistics

Applied Statistical Modeling is offered as a second course in statistics in which we present a set of case studies and introduce appropriate statistical modeling techniques for each. Topics may include: multiple linear regression, logistic regression, log-linear regression, survival analysis, an introduction to Bayesian modeling, and modeling via simulation. Other topics may be substituted for these or added as time allows. Students are expected to conduct data analyses in R.

This course is intended to introduce you to the practice and art of statistical modeling. We will introduce the relevant concepts by exploring model building on real data, studying how to talk and think about the process of addressing scientific questions with statistical methods.

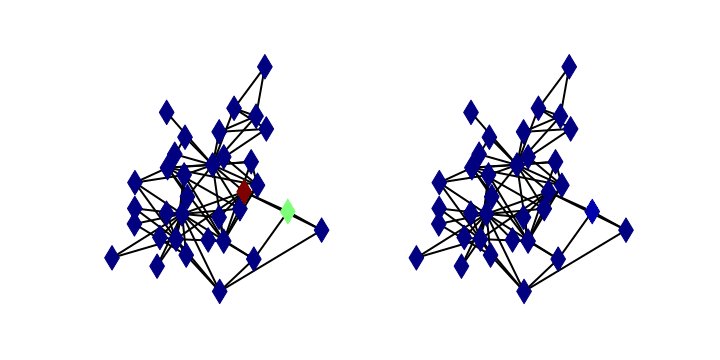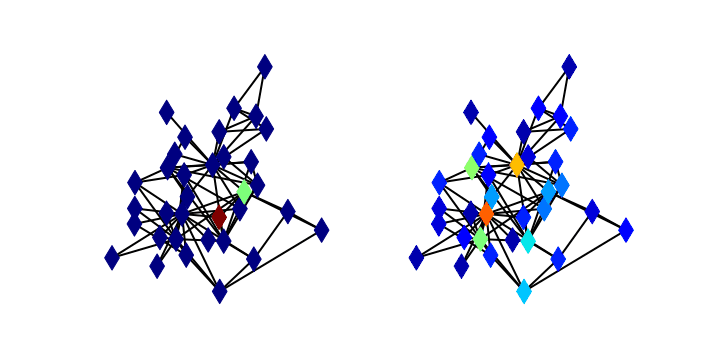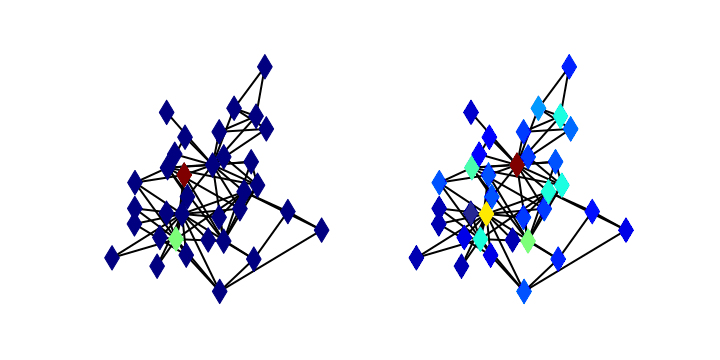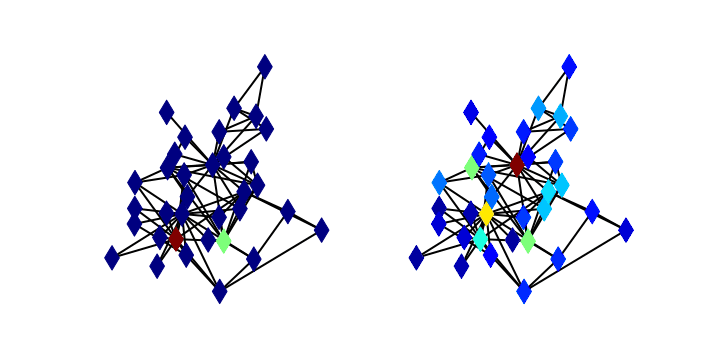
This course introduces statistical tools, theory, and methodology for analyzing complex social systems with network models. Students are introduced to standard network constructions and associated centrality metrics, clustering algorithms, and dynamical models through classic papers and examples. A main focus of the course is generative models for social network data and the theory and computation of associated inference problems, including MCMC sampling. In addition to the Erdos-Renyi and stochastic block models, special attention ispaid to the family of Exponential Random Graph Models and Latent Space models, which have found significant applications across the social sciences in recent years. Students will gain experience performing inference and doing analysis on real data using R.